Tips 1: Hvordan finne grunnlaget for en trapes
Tips 1: Hvordan finne grunnlaget for en trapes
Basene av trapesen finnes i fleremetoder, avhengig av de angitte parametrene. For et kjent område, høyde og side av en like-sidig trapezzo, reduseres sekvensen av beregninger for å beregne sidene av en ensell trekant. Og også til bruken av eiendommen til en isosceles trapes.

instruksjon
1
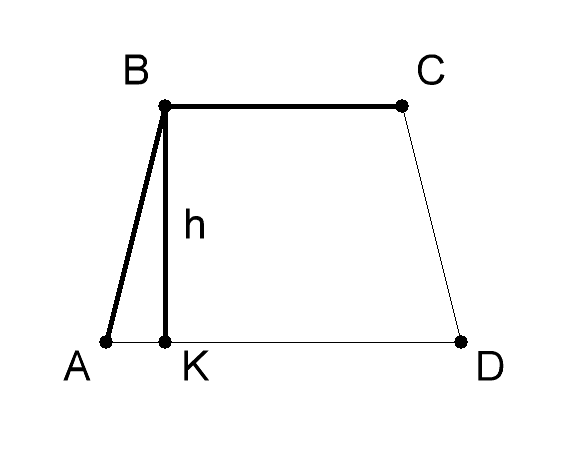
Tegn en like-sidig trapezoid. Gitt trapesformens område - S, trapesformens høyde og siden - a. Senke trapesens høyde til en større base. Den større basen vil bli delt inn i segmentene m og n.

2
For å bestemme lengden på begge basene (x, y), bruk egenskapen til en like-sidig trapesform og formelen for å beregne området av trapesformet.
3
Ifølge eiendommen til et ensartet trapes, segmentet ner lik halvforskjellen mellom basene x og y. Følgelig kan den mindre basen av trapesformet y representeres som forskjellen på den større basen og segmentet n multiplisert med to: y = x - 2 * n.

4
Finn det ukjente, mindre segmentet n. For å gjøre dette, beregne du en side av den resulterende høyre trekanten. Triangelet er dannet av høyden - k (katetre), side - a (hypotenuse) og segmentet - n (katetre). Ifølge pythagorasetningen, den ukjente katedralen n² = a² - h². Erstatt de kjente tallverdiene og beregne kvadratet av benet n. Ta kvadratroten av den resulterende verdien - dette er lengden på segmentet n.

5
Erstatt denne verdien i den første ligningen for å beregne y. Trapesformens område beregnes med formelen S = ((x + y) * h) / 2. Express den ukjente variabelen: y = 2 * S / h - x.

6
Ta opp begge mottatte ligninger i systemet. Ved å erstatte de kjente verdiene, finn de to ukjente mengdene i systemet med to ligninger. Den resulterende løsningen av systemet x er lengden på den større basen, og y er den mindre basen.

Tips 2: Hvordan finne lengden på basen av trapesen
For å spesifisere et slikt firkant som en trapesform, må minst tre av sidene defineres. Derfor kan vi for eksempel vurdere et problem hvor lengdene på diagonalene er gitt trapes, og også en av vektorene på siden.

instruksjon
1
2
Tenk på trekanten ABD. Lengden på sin side AB er lik modulen til vektoren a. Anta at | a | = sqrt ((akse) ^ 2 + (ay) ^ 2) = a, deretter cosφ = ax / sqrt (((akse) ^ 2 + (ay) ^ 2) som ledende cosinus av a. diagonal BD har lengde p, og ønsket AD lengde x. Deretter, etter cosinus teorem, P ^ 2 = a ^ 2 + x ^ 2-2axcosf. Eller x2 2axcosφ + (a ^ 2-p ^ 2) = 0.
3
Løsninger av den kvadratiske ligning: X1 = (2acosf + sqrt (4 (a ^ 2) ((cos) ^ 2) -4 (a ^ 2-p ^ 2))) / 2 = acosf + SQRT ((a ^ 2) ((cos) ^ 2) - (a ^ 2-p ^ 2)) == a * øks | sqrt (((ax) ^ 2 + (y) ^ 2) + sQRT ((((a) ^ 2) (økse ^ 2)) / (ax ^ 2 + ay ^ 2)) - a ^ 2 + p ^ 2) = AD.
4
Å finne den øvre begrunnelse BC (lengden i søket etter løsningen er også betegnet med x), modulen | a | = a brukes, og også den andre diagonale BD = q og cosinus av vinkelen ABC, som tydeligvis er lik (n-φ).
5
Trianglen ABC, ksom, som tidligere, er cosinus teorem påført, og følgende løsning oppstår. Med tanke på at cos (n-φ) = -cosφ, på basis av løsningen for AD, kan vi skrive følgende formel, erstatte p ved q: BC = - a * ax | sqrt (((ax) ^ 2 + (ay) ^ 2 ) + sqrt ((((a) ^ 2) (ax ^ 2)) / (ax ^ 2 + ay ^ 2)) - a ^ 2 + q ^ 2).
6
Denne ligningen er firkantet og,Følgelig har to røtter. Således er det i dette tilfellet bare å velge de røttene som har en positiv verdi, siden lengden ikke kan være negativ.
7
PrimerPust i trapes ABCD-siden av AB er gitt av vektoren a (1, sqrt3), p = 4, q = 6. finne begrunnelse trapesOppløsning. Ved å bruke algoritmene oppnådd ovenfor kan vi skrive: | a | = a = 2, cosφ = 1/2. AD = 1/2 + sqrt (4/4 -4 + 16) = 1/2 + sqrt (13) = (sqrt (13) +1) /2.BC=-1/2+sqrt (-3 + 36 ) = (sqrt (33) -1) / 2.
Tips 3: Hvordan finne trapezens høyde
En trapezoid er en firkant, yhvilke to sider er parallelle, og de andre to er ikke. Trapesens høyde er segmentet trukket vinkelrett mellom to parallelle linjer. Avhengig av de opprinnelige dataene kan den beregnes på forskjellige måter.
Du trenger
- Kunnskap om sidene, basene, midtlinjen til trapesen, samt eventuelt dens område og / eller omkrets.
instruksjon
1
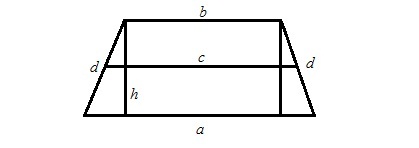
En måte å beregne området på trapesener produktet av høyden og midtlinjen. Anta at det er en likestillende trapes. Deretter beregnes høyden på et ensartet trapes med baser a og b, areal S og omkrets P som følger: h = 2 x S / (P-2 x d). (se figur 1)
2
Hvis bare et visst område av trapesens og dens basis, kan høyden beregningsformel utledes fra området av et trapes formel S = 1 / 2t x (a + b): h = 2S / (a + b).
3
Anta at det er en trapes med samme data somog i figur 1. Vi tegner 2 høyder, vi får et rektangel, hvor de to mindre sidene er beina av rettvinklede trekanter. La oss betegne den minste for x. Det er funnet ved å dele forskjellen i lengde mellom de store og mindre basene. Da, ved pythagorasetningen, er høydepunktet lik summen av rutene i hypotenus d og røntgenstrålen. Vi trekker ut roten fra denne summen og får høyden h. (Figur 2)

Tips 4: Hvordan finne grunnene til en rektangulær trapesform
En matematisk figur med fire hjørner kalles en trapezoid hvis paret av motsatte sider er parallelle, og det andre paret er ikke. Parallelle sider kalles baser trapes, den andre to-sidene. I en rektangulær trapes en av vinklene på siden er rett.

instruksjon
1
Oppgave 1. Finn basene av BC og AD rektangulær trapeshvis lengden på diagonal AC = f er kjent; lengdesideveis CD = c og vinkelen med den ADC = α. Løsning: Vurder den rektangulære trekant CED. Kjent hypotenuse c og vinkelen mellom hypotenus og benet på EDC. Finn lengdene på sidene CE og ED: i henhold til vinkelformelen CE = CD * sin (ADC); ED = CD * cos (ADC). Så: CE = c * sinα; ED = c * cosa.
2
Vurder den rette triangelen ACE. Hypotenusen AC og CE beinet du vet, får den siden AE av regelen av en rettvinklet trekant: summen av kvadratene av bena er lik kvadratet av hypotenusen. Så: AE (2) = AC (2) - CE (2) = f (2) - c * sinα. Beregn kvadratroten på høyre side av ligningen. Du fant den øverste basen av en rektangulær trapes.
3
Lengden på basen AD er summen av lengdene på tosegmenter AE og ED. AE = kvadratroten (f (2) - c * sinα); ED = c * cosα). Så: AD = kvadratroten (f (2) - c * sinα) + c * cosα. Du fant den nederste bunnen av en rektangulær trapes.
4
Oppgave 2. Finn basene av BC og AD rektangulær trapeshvis lengden på diagonal BD = f er kjent; lengdesideveis CD = c og vinkelen med den ADC = α. Løsning: Vurder den rektangulære trekant CED. Finn lengdene på CE- og ED-sidene: CE = CD * sin (ADC) = c * sinα; ED = CD * cos (ADC) = c * cosa.
5
Vurder ABCE-rektangelet. Ved egenskapen til rektangelet AB = CE = c * sinα. Overvei høyre trekant ABD. Ved egenskapen av en riktig trekant er torget av hypotenus lik summen av rutene på bena. Derfor, AD (2) = BD (2) - AB (2) = f (2) - c * sinα. Du fant den nederste bunnen av en rektangulær trapes AD = kvadratrot (f (2) - c * sinα).
6
Ved regelen rektangelet BC = AE = AD - ED = kvadratroten (f (2) - c * sinα) - c * cosα.Vy funnet rektangulær øvre basis trapes.
Tips 5: Hvordan finne den mindre siden av trapesen
Trapesens mindre base er en av sine parallelle sider, som har en minimumslengde. Beregn denne verdien på flere måter, ved å bruke visse data.

Du trenger
- - kalkulator.
instruksjon
1
Hvis to lengder er kjent - en stor basetrapes og midtlinje - bruk trapesegenskapen til å beregne den minste basen. Ifølge ham er trapesformens midtlinje identisk med halvparten av basene. I dette tilfellet vil den minste basen være lik forskjellen mellom den doble lengden på midtlinjen og lengden på den store basen av denne figuren.
2
Hvis du kjenner slike trapesformige parametere somområde, høyde, lengde på en stor base, og deretter beregne den minste basis av denne figuren basert på trapesformet formel. I dette tilfellet oppnås det endelige resultatet ved å trekke fra forskjellen mellom det angitte dobbeltarealet og høyden av en slik parameter som lengden av den store basen av trapesformen.
3
Lengden på den minste siden i en rektangulærTrapes beregnes med en annen metode. Denne parameteren vil være lik produktet av lengden på den andre siden og sinusen i den spisse vinkelen ved siden av den. I samme tilfeller, når verdien av vinkelen er ukjent, må du likestille den minste side siden til trapesens høyde og beregne den i henhold til Pythagorasetningen. Den minste siden i den rektangulære trapesen er funnet ved hjelp av cosinus teorem: c² = a² + b²-2ab * cosα; hvor a, b, c representerer sidene av trekanten; α er vinkelen mellom sider a og b.
Tips 6: Hvordan finne den minste høyden på en trekant
I trekanten er forholdet mellom sidene og hjørnene stift forbundet også med de indre linjene i figuren - høyder, medianer og bisektorer. Kunnskap om disse relasjonene forenkler problemløsningen i stor grad.

instruksjon
1
Av de tre høyder av trekanten,som senkes til den største av sidene av figuren. For å se dette, uttrykk alle tre høyder av trekanten gjennom dimensjonene på sidene og sammenlign. Anta at siden a er den største av de tre sidene a, b, c av en vilkårlig akuttvinklet trekant, siden c er den minste. Vi betegner høyden h på siden a, hb høyden trukket til siden b, hc høyden til siden c. Høyde deler hver trekant i to rektangulære trekanter, hvor denne høyden alltid vil være en av bena.
2
Høyden ha, trukket til den største siden av a,kan bestemmes av pythagorasetningen: hâ² = b² - а²² eller hа² = с² - а²². Hvor a1 og a2 er de segmentene som siden a er delt av høyde ha. Også, ved Pythagorasetningen, uttrykker de to andre høyder av trekanten gjennom sidene: hb ² = a²-b₁² eller hb² = c²-b₂²; hc² = a²-c₁² eller hc² = b²-c2².
3
Fra en sammenligning av formlene som bestemmer høydenetrekant, er det tydelig at forholdet mellom minuend og subtrahend gir den minste forskjell når det gjelder ha² = b² - a₁² og ha² = s²-a₂² som berettiget a ^ og a₂ - største sidelengder av en trekant.
4
For å bestemme den minste høyden på trekanten, kan duogså gjennom sinus av den kjente vinkelen av trekanten. Hvis betingelsen er den største av vinklene, så ligger denne vinkelen mot den største siden, og fra den minste høyde trekkes. For å unngå omstendelige beregninger bedre uttrykker den ønskede høyden via de trigonometriske funksjoner av de to andre vinkler i trekanten, fordi forholdet av trekanten til sinus til den motstående vinkel - verdi for en gitt trekant er konstant. Følgelig er den minste trekant høyden ha = b * SinB eller ha-= c * sinc, hvor B er vinkelen mellom den største side en side og b, og c - vinkelen mellom den høyeste side og den side og trekanten.