Tips 1: Hvordan finne bøyningsradius av bane
Tips 1: Hvordan finne bøyningsradius av bane
Når man vurderer kroppens bevegelse, er en rekkekarakterisere mengdene, for eksempel tangentiell og normal (centripetal) akselerasjon, hastighet og også krumning av banen. Krumningsradius er et geometrisk konsept som angir radiusen til sirkelen R langs hvilken kroppen beveger seg. Denne parameteren kan bli funnet fra de tilsvarende formlene ved å bruke den angitte banen.

instruksjon
1
De vanligste oppgavene er å bestemmeKrumningsradius for bane av flyet av den forlatte kroppen i et gitt tidsintervall. Banen av bevegelsen i dette tilfellet er beskrevet ved ligningene på koordinataksene: x = f (t), y = f (t), hvor t - den tid i hvilken den tid som er nødvendig for å finne den radius. Beregningen vil baseres på å anvende formelen an = V² / R. Her avsløres radiusen R fra forholdet mellom den normale akselerasjon an og den øyeblikkelige hastigheten V av kroppsbevegelsen. Etter å ha lært disse dataene, kan du enkelt finne den ønskede komponenten R.
2
Beregn projeksjonene av kroppens hastighet på aksene (OX, OY). Den matematiske betydningen av fart er det første avledet av bevegelsens ligning. Derfor er de lett funnet ved å ta derivatet av de gitte ligningene: Vx = x ", Vy = y". Når man undersøker den geometriske kartleggingen av projeksjonsdata i koordinatsystemet, er det klart at de er beina til en riktig trekant. Og hypotenusen i den - den ønskede øyeblikkelige hastigheten. Ut fra dette beregner du den øyeblikkelige hastigheten V ved Pythagorasetningen: V = √ (Vx² + Vy²). Ved å erstatte uttrykket en kjent verdi av tid, finn den numeriske verdien av V.
3
Den normale akselerasjonsmodulen er også enkelbestemme ved å vurdere en annen rektangulær trekant dannet av absolutt akselerasjonsmodul a og tangentiell akselerasjon av kroppen ak. Og her er normal akselerasjon et ben og beregnes som følger: an = √ (а² - ак²). For å finne tangentiell akselerasjon, differensierer momentan hastighetsligningen etter tid: ak = | dV / dt |. Beregn den samme akselerasjonen fra projeksjonene på aksen, ligner på å finne den øyeblikkelige hastigheten. Bare for dette formålet, ta fra de gitte bevegelsesligningene andreords-derivatene: ax = x ", ay = y". Akselerasjonsmodulen er a = √ (ax2 + ay2). Ved å erstatte alle funnet verdier, bestem tallverdien for normal akselerasjon an = √ (а² - ак²).
4
Uttrykk fra formelen an = V2 / R den nødvendige variabelen av krumningsradius av kurven: R = V² / an. Erstatt tallverdiene for hastighet og akselerasjon, beregne radius.
Tips 2: Hvordan finne krumningsradius
Kurvatur er et konsept lånt fradifferensial geometri. Det er det kollektive navnet på en hel serie kvantitative egenskaper (vektor, skalar, tensor). Krumningen av de geometriske avvik indikerer "objekt", som kan være flate og kurven, og en Riemann plass, andre kjente "flat" gjenstander (fly, linje, euklidske plass, og D. osv.).

instruksjon
1
Vanligvis bestemmes krumningen separat forav hvert ønsket punkt på et gitt "objekt" og betegne det som andreordens verdi av differensialuttrykket. For objekter med redusert glatthet kan krumningen også bestemmes i den integrerte forstand. Som en generell regel, hvis i det hele tatt krumning identiteten er null, da dette innebærer en lokal tilfeldighet av det gitte "objektet" med "flat" objektet.
2
La oss si at du må lage en plano-konveks linse. Du vet bare at den optiske kraften er 5 dpt. Hvordan finne radius krumning konveks overflate av en gitt linse.Tilbakekalling ligning: D = 1 / fD - en optisk effekt (en linse), f - er det sentrale rasstoyanieZapishite ligning: 1 / f = (n-1) * (1 / R1 + 1 / R2) n - er brytningsindeksen (av typen materiale) r1 - radius linser på den ene siden av den - på den annen side
3
Forenkle uttrykket: siden linsen er plan-konveks, er dens radius med en av sidene vil ha en tendens til uendelighet, da 1, delt av uendelig, vil ha en tendens til null. Du bør få dette forenklede uttrykket: 1 / f = (n-1) * 1 / r2
4
Siden du kjenner den optiske effekten av et objektiv, finn ut brennvidden: D = 1 / f1 / f = 5 dptf = 1/5 dptf = 0,2 m
5
Gitt oppgaven, lage et objektiv av glass. Husk at brytningsindeksen til glasset er 1,5, og dermed uttrykket du skal se slik ut: (1,5 - 1) * 1 / r2 = 0,2 m0,5 * 1 / r2 = 0,2 m
6
Del alle deler av dette uttrykket med 0,5. Du bør få: 1 / r2 = 0.4 mr2 = 1 / 0.4 mr2 = 2.5 m Skriv resultatet: D. Du får en flat-konveks linse radius krumning 2,5 meter.
Tips 3: Hvordan finne radius
Hvis det er en polygon, er det mulig å konstruereinnskrevet og begrenset omkrets, er området til denne polygonen mindre enn den omkretsede omkretsen, men større enn området for den innskrevne sirkel. For noen polygoner er formler kjent for å finne av radiusen innskrevne og omskrevne sirkler.

instruksjon
1
Inskrevet i en polygon er en sirkel som berører alle sider av polygonen. For en trekant, formel av radiusen innskrevet sirkel: r = ((p-a) (p-b) (p-c) / p) ^ 1/2, hvor p er semipimeteret; a, b, c er sidene av trekanten. For en vanlig trekant forenkles formelen: r = a / (2 * 3 ^ 1/2), og a er siden av trekanten.
2
Polygonen er beskrevet rundt detteEn sirkel hvor alle polygonens hjørner ligger. For en trekant er radiusen for den omkretsede sirkelen funnet ved formelen: R = abc / (4 (p (p-a) (p-b) (p-c)) 1/2) hvor p er halvperimeteren; a, b, c er sidene av trekanten. For en vanlig trekant er formelen enklere: R = a / 3 ^ 1/2.
3
For polygoner er det ikke alltid mulig å finne utforholdet mellom radier av innskrevne og begrensede omkretser og lengdene av dets sider. Det er ofte begrenset til å bygge slike sirkler rundt et polygon, og deretter en fysisk måling av radiusen sirkler ved hjelp av måleinstrumenter ellervektor plass. For å konstruere circumcircle av en konveks polygon, konstruere bisectors av to av sine vinkler, ved krysset som ligger midt i den omkranset sirkel. Radien er avstanden fra skjæringspunktet mellom bisektorene til vertexet av hvert hjørne av polygonen. Midtpunktet av den innskrevne sirkel ligger i skjæringspunktet mellom perpendikulærene bygget innover fra polygonen fra sidens sentre (disse perpendikulærene kalles de midterste). Det er nok å bygge to slike perpendicularer. Radius av den innskrevne sirkel er lik avstanden fra skjæringspunktet mellom median perpendikulærene til siden av polygonen.
Tips 4: Hvordan finne radius av en sirkel
definisjon av radiusen sirkel er en av de viktigste oppgavene til matematikk. Det er mange formler for regnskap av radiusen, det er nok å bare vite noen standardparametere. Grafisk er radius betegnet med bokstaven R i det latinske alfabetet.

instruksjon
1
En sirkel er en lukket kurve. Poengene i flyet er like langt fra midten som ligger i samme plan sammen med kurven. Radius - segment sirkel, koble sitt senter med noen av sine punkter. Med hjelpen kan du lære mange andre parametere i figuren, så det er en viktig parameter. Den numeriske verdien av radiusen vil være lengden på dette segmentet.
2
Det er også nødvendig å skille radius av en figur fra dens diameter (diameteren forbinder to punkter så langt fra hverandre som mulig fra hverandre). Å bruke matematisk metode for å finne av radiusen Du må vite lengden eller diameteren sirkel. I det første tilfellet vil formelen se ut som "R = L / 2?", Hvor L er den kjente lengden sirkel, og nummeret? er lik 3,14 og brukes til å betegne et bestemt irrasjonelt tall.
3
I tilfelle at bare diameteren er kjent, vil formelen se ut som "R = D / 2".
4
Hvis lengden sirkel Ukjent, men det er data på lengde og høydebestemt segment, så formelen vil ha formen «R = (h ^ 2 * 4 + L ^ 2) / 8 * h», hvor h - høyde av det segment (er avstanden fra midten av korden til den mest utstikkende del av det nevnte gnist), og L - Stykkets lengde (som ikke er en kordelengde) .Horda - et linjesegment som forbinder to punkter sirkel.
Tips 5: Hvordan finne den øyeblikkelige hastigheten
Å finne øyeblikkelig fart på en jevn bevegelse deles avstanden som reist av kroppen, for den tiden det ble overvunnet for. Hvis det er ujevn bevegelse, finn ut akselerasjonsverdien og tellingen fart på hvert øyeblikk av tid. Ved et fall, øyeblikkelig fart Avhenger av akselerasjonen av fritt fall og tid. momentant fart kan måles med et speedometer eller radar.

Du trenger
- For å bestemme den øyeblikkelige hastigheten, ta en radar, et hastighetsmålere, et stoppeklokke, et målebånd eller en rekkeviddefinder, et akselerometer.
instruksjon
1
Bestemmelse av øyeblikkelig hastighet på uniformHvis kroppen beveger seg jevnt, måle avstanden i meter i en roulette- eller rangefinder, og del deretter den oppnådde verdien med tidsintervallet i sekunder for hvilket dette segmentet ble passert. Mål tid med stoppeklokke. Finn deretter gjennomsnittet fart, dividere sti lengden med tiden det går (v = s / t). Og siden bevegelsen er jevn, er gjennomsnittet fart vil være lik den øyeblikkelige hastigheten.
2
Bestemmelse av øyeblikkelig hastighet ved ikke-uniformDen viktigste typen ikke-uniform bevegelse er den jevnt akselererte bevegelsen. Bruk akselerometer eller annen metode for å måle akselerasjonsverdien. Etter dette, å vite den første fart bevegelse, legg til det produktet av akselerasjonog tiden hvor kroppen er i bevegelse. Resultatet er øyeblikkelig fart på et gitt tidspunkt. (v = v0 + a • t). Når du regner med, merk at hvis kroppen minker dens fart (hemmer), vil akselerasjonsverdien være negativ. Hvis bevegelsen starter fra hvilemodus, er den første fart er lik null.
3
Bestemmelse av øyeblikkelig hastighet med friFor å bestemme den øyeblikkelige hastigheten til et fritt fallende legeme, skal falltiden multipliceres med akselerasjon på grunn av tyngdekraften (9,81 m / s²), og beregningen skal gjøres ved å bruke formelen v = g • t. Vær oppmerksom på at med fri fall, den første fart kroppen er null. Hvis kroppen faller fra en viss høyde, må du for å bestemme den øyeblikkelige hastigheten når den faller fra denne høyden multiplisere verdien i meter med tallet 19.62, og fra det resulterende tallet, trekk ut kvadratroten.
4
Bestemmelse av øyeblikkelig hastighet med et speedometer eller radar Hvis den bevegelige kroppen er utstyrt med et hastighetsmåler (bil), vil dets skala eller elektronisk resultattavle kontinuerlig vise en øyeblikkelig fart på et gitt tidspunkt. Når du observerer kroppen fra et fast punkt (jord), pek på radarsignalet på det, displayet vil vise en øyeblikkelig fart kroppen på et gitt tidspunkt.
Tips 6: Hvordan bestemme krumningsradiusen
Å studere bevegelsen til noen fysiskeobjekt (bil, sykler, ball i roulette) det er nok å studere bevegelsen av noen av poengene sine. Når du studerer bevegelsen, viser det seg at alle punkter beskriver noen buede linjer.

instruksjon
1
Vet at kurver kan beskrive bevegelsenflytende, gass, lysstråler, strømlinjeformer. Krumningsradius for en plankurve ved et bestemt punkt er radius av tangenskretsen på dette punktet. I noen tilfeller er kurven gitt ved ligninger, og krumningsradiusen beregnes med formlene. Følgelig, for å finne radius av kurvatur, er det nødvendig å kjenne radius av en sirkel knyttet til et visst punkt.
2
Bestem punktet A på kurveplanet, ta et annet punkt B. Tegn tangentene til den eksisterende kurven som passerer gjennom punktene A og B.
3
Pass gjennom punktene A og B,Vinkelrett på den konstruerte tangenten, strekk dem til krysset. Angi krysspunktet for perpendikulærene som 0. Poenget O er midten av tangenskretsen på et gitt punkt. Derfor er OA radius av sirkelen, dvs. krølling ved et gitt bestemt punkt A.
4
Vær oppmerksom på at når et punkt beveger seg langs en krøllete bane på et hvilket som helst bevegelsesmoment, beveger det seg langs en sirkel som varierer fra punkt til punkt.
5
Hvis for et punkt i rommet for å bestemme kurvaturenei to innbyrdes vinkelrett retninger, vil disse kurvaturene bli kalt hovedstol. Retningen av hovedkrumninger må være nødvendigvis 900. For beregning bruker ofte en gjennomsnittlig krumning lik halvparten av summen av de viktigste kurvaturer, og den Gaussiske krumning som tilsvarer deres produkt. Det er også begrepet kurvatur av en kurve. Dette er gjensidig av krumningsradius.
6
Accelerasjon er en viktig faktor i bevegelsen av punktet. Banens krumning påvirker direkte akselerasjonen. Accelerasjon oppstår når et punkt med konstant hastighet begynner å bevege seg langs en kurve. Ikke bare endrer den absolutte størrelsen på hastigheten, men også dens retning, det er en centripetal akselerasjon. dvs. i virkeligheten begynner punktet å bevege seg langs sirkelen, som berører på et gitt tidspunkt.
Tips 7: Hvordan finne normal akselerasjon
Normal akselerasjon observeres i tilfelle,når kroppen beveger seg langs omkretsen. Og denne bevegelsen kan være jevn. Denne akselerasjonens karakter er knyttet til det faktum at kroppen som beveger seg langs sirkelen, endrer hastighetenes retning, siden den lineære hastigheten er tangentiell til hvert punkt i sirkelen.

Du trenger
- hastighetsmåler eller radar, stoppeklokke, rekkeviddefinder.
instruksjon
1
Bruk en hastighetsmåler eller radar, måler den lineæreHastighet på kroppen som beveger seg langs omkretsen. I området måler du radius. For å finne normal akselerasjon av en kropp som beveger seg langs en sirkel, ta hastighetsverdien til en bestemt tid, kvadrat den og divisjon med radiusen til sirkelen av bevegelsesveien: a = v² / R.
2
Hvis vinkelhastigheten til kroppen er kjent under bevegelsen,Finn den normale akselerasjonen ved å bruke verdien. For dette formål løftes kvadratisk vinkelhastighet og dividere med den sirkelradius ved hvilken det bevegelige legeme: a = ω² • R.Esli ikke mulig å måle hastigheten av et legeme som beveger seg i en sirkel, beregne det ved rotasjon periode. For å finne den skifteperioden, ved hjelp av en stoppeklokke, måle den tid i løpet av hvilken legemet vender tilbake til utgangspunktet. Hvis kroppen beveger seg for fort, måler du tiden der flere fulle kroppsomsving blir gjort. Den resulterende tids dividere med antall rotasjoner og motta tid av en omdreining, som kalles rotasjonsperiode. Tiden måles i sekunder. For å finne den normale akselerasjonen, divisjon nummer 6.28 ved rotasjonsperioden av kroppen. Det resulterende nummer kvadreres og formere seg på radien i sirkelen på hvilken det bevegelige legeme: a = (6,28 / T) ² • R.
3
Den normale akselerasjonen kan måles ved å kjenne frekvensenrotasjon av kroppen. For å beregne frekvensen, del en rekke rotasjoner av tiden i sekunder, for hvilke de forekommer. Resultatet er antall rotasjoner per sekund - dette er frekvensen. Beregn normal akselerasjon av kroppen, multipliserer tallet 6.28 ved frekvensen av rotasjonen, det resulterende tallet er kvadret. Multipliser resultatet ved radiusen av sirkelen langs hvilken kroppen beveger seg: a = (6.28 • υ) ² • R.
Tips 8: Hvordan finne krumningsradius
La det bli gitt en funksjon definert av ligningen y =f (x) og tilhørende graf. Det kreves å finne radius av kurvaturen, det vil si å måle kurvgraden av grafen for denne funksjonen på et tidspunkt x0.

instruksjon
1
Krumningen av en hvilken som helst linje bestemmes av hastighetenrotasjon av tangenten ved punktet x når dette punktet beveger seg langs kurven. Ettersom helningen til tangenten er lik verdien av den deriverte av f (x) på dette punkt, vil endringstakten for denne vinkelen er avhengig av den andre deriverte.
2
Krumningsstandarden er logisk for å akseptere en sirkel,Siden det er jevnt buet gjennom hele lengden. Radien av en slik sirkel er måleverdien av krumningen. I analogi er krumningsradiusen for en gitt linje ved punktet x0 radius av sirkelen, som mest nøyaktig måler krumningsgraden på dette punktet.
3
Den nødvendige sirkelen må være i kontakt medgitt kurve i punktet x0, dvs. på den side av sin konkavitet, slik at tangenten til kurven ved dette punktet var også tangent til sirkelen. Dette betyr at hvis F (x) - ligningen av sirkelen, deretter likheter: F (x0) = f (x0), F '(x0) = f' (x0) .such sirkler, selvsagt, det er uendelig mange. Men for å måle krumningen, er det nødvendig å velge den som nærmest tilsvarer den gitte kurven på dette punktet. Ettersom krumningen måles ved hjelp av den andre deriverte, da disse to ligninger er nødvendig for å legge til en tredje: F '' (x0) = f '' (x0).
4
På grunnlag av disse forhold, er krumningsradien beregnet ved formelen: R = ((1 + f '(x0) ^ 2) ^ (3/2)) / (| f' '(x0) |) .Velichina, invers krumningsradius, kalles krumning av linjen på et gitt punkt.
5
Hvis f (x0) = 0, er krumningsradiusenuendelig, det vil si linjen på dette punktet er ikke buet. Dette gjelder alltid for rette linjer, så vel som for eventuelle linjer ved bøyningspunkter. Krumningen ved henholdsvis slike punkter er null.
6
Senteret av sirkelen som måler krumningen av linjen på et gitt punkt kalles krumningspunktet. En linje som er et geometrisk lokus for alle krøllingspunktene for en gitt linje kalles dens evolusjon.
Tips 9: Hvordan finne centripetal akselerasjon
Sentripetal akselerasjon oppstår nårbevegelsen av kroppen langs omkretsen. Den er rettet til sentrum, målt i m / s². En funksjon av denne typen akselerasjon er at den eksisterer selv når kroppen beveger seg med konstant fart. Det avhenger av sirkelens radius og kroppens lineære hastighet.

Du trenger
- - Hastighetsmåler;
- - En enhet for måling av avstand
- - Stoppeklokke.
instruksjon
1
For å finne centripetalakselerasjon, måle hastigheten til en kropp som beveger seg langs en sirkulær bane. Du kan gjøre det med et speedometer. Hvis dette ikke er mulig, beregne linjens hastighet. For å gjøre dette, legg merke til tiden som ble brukt for en komplett revolusjon langs en sirkulær bane.
2
Denne tiden er rotasjonsperioden. Express det om noen sekunder. Mål radiusen til sirkelen langs hvilken kroppen beveger seg med en linjal, et målebånd eller en laseravstandsmåler i meter. For å finne hastigheten, finn produktet av nummer 2 med tallet π≈3,14 og radius R av sirkelen, og del resultatet med perioden T. Dette vil være kroppens lineære hastighet v = 2 ∙ π ∙ R / T.
3
Finn centripetal akselerasjon a, delingkvadratet av den lineære hastigheten v ved radiusen av sirkelen langs hvilken legemet R (ay = v2 / R) beveger seg. Bruk formlene for å bestemme vinkelhastigheten, frekvensen og rotasjonsperioden, finn denne verdien ved hjelp av andre formler.
4
Hvis vinkelhastigheten ω er kjent, og radiusen(omkretsen langs hvilken kroppen beveger seg) R, så vil centripetal akselerasjonen være lik az = ω2 ∙ R. Når kjente legeme rotasjon periode T, og radien av banen R, ATS = 4 ∙ π² ∙ R / T². Dersom det kjent hastighet ν (antall hele omdreininger per sekund), og deretter bestemme sentripetal akselerasjon ved formelen = 4 ats ∙ π² ∙ R ∙ ν².
5
eksempel: Bilen, hvis hjulradius er 20 cm, beveger seg langs veien med en hastighet på 72 km / t. Bestem centripetal akselerasjon av de ekstreme punktene til hjulene. Løsning: Den lineære hastigheten til punktene på et hjul er 72 km / h = 20 m / s. Vri radius av hjulet i meter R = 0,2 m. Beregn centripetal akselerasjon, ved å erstatte de resulterende dataene i formelen az = v² / R. Få az = 20² / 0,2 = 2000 m / s². Denne sentripetale akselerasjonen med jevn rettlinjet bevegelse vil være på de ytterste punktene i alle fire hjul i bilen.
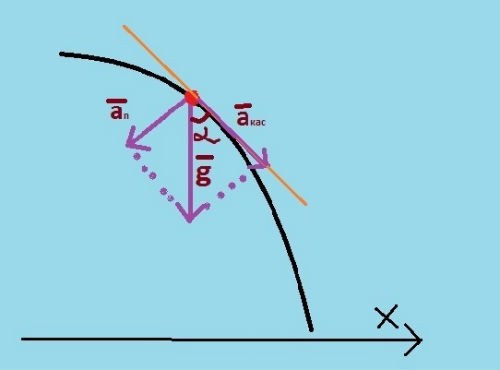
Tips 10: Hvordan finne tangentiell akselerasjon
tangentiell akselerasjon forekommer i legemer som beveger seg langs en krølletebane. Det er rettet i retning av å endre kroppens hastighet langs tangenten til bevegelsesbanen. Tangentiell akselerasjon forekommer ikke i legemer som beveger seg jevnt langs omkretsen, de har bare en centripetal akselerasjon.
Du trenger
- - hastighetsmåler eller radar;
- - linjal eller målebånd
- - Stoppeklokke.
instruksjon
1
Finn tangentiell akselerasjon aτ hvisEn fullstendig akselerasjon av punktet som beveger seg langs den krøllete bane a og dens sentripetale akselerasjon er kjent. For dette formål, er kvadratet av hele akselerasjons subtrahere kvadratisk sentripetal akselerasjon, og den oppnådde verdi av kvadratroten ekstrakt aτ = √ (a²-an²). Når sentripetal akselerasjon er ukjent, men det er den øyeblikkelige hastighet, en linjal eller bånd måle krumningsradien for banen og lokalisere dens verdi ved å dividere kvadratet av den øyeblikkelige hastighet v, som måler radaren speedometer eller på krumningsradien av banen R, an = v² / R.
2
Et eksempel. Kroppen beveger seg langs en sirkel med en radius på 0,12 m. Den totale akselerasjonen er 5 m / s², bestemmer dens tangentielle akselerasjon på et tidspunkt når hastigheten er 0,6 m / s. Først finner du centripetal akselerasjon av kroppen ved den angitte hastigheten, for dette dividerer plassen ved radiusen av banen a = v² / R = 0,6² / 0,12 = 3 m / s². Finn tangentiell akselerasjon med formelen aτ = √ (a²-an²) = √ (5²-3²) = √ (25-9) = √16 = 4 m / s².
3
Bestem mengden tangentiell akselerasjongjennom endringen i hastighetsmodulet. For å gjøre dette, bruk hastighetsmåleren eller radaren til å bestemme kroppens innledende og siste hastighet i en viss tidsperiode, som du måler ved hjelp av stoppeklokke. Finn tangentiell akselerasjon ved å subtrahere initialverdien av hastigheten v0 fra den endelige v og dividere den med tidsintervallet t, der denne endringen oppstod: aτ = (v-v0) / t. Hvis verdien av tangentiell akselerasjon er negativ, vil kroppen bremse, hvis positiv - akselererer.
4
Et eksempel. I 4 s reduserte kroppens hastighet langs omkretsen fra 6 til 4 m / s. Bestem dens tangentielle akselerasjon. Bruk beregningsformelen, få aτ = (v-v0) / t = (4-6) / 4 = -0,5 m / s². Dette betyr at kroppen senkes med en akselerasjon hvis absoluttverdi er 0,5 m / s².
Tips 11: Hva er krumningsradiusen til objektivet
Krumningsradiusen for kontaktlinser er en parameter,som bestemmer størrelsen deres. Hvis den blir plukket opp feil, vil en person oppleve ulemper når han bærer slike linser, og hans syn kan forverres betydelig.

Hvordan er krumningsradien til objektivet
Krumningsradiusen til objektivet vil avhenge av strukturenmenneskelige øyebuer. Siden linsen er plassert på hornhinnen i øyet, må den gjenta sin form så nøyaktig som mulig. Eple menneskelige øye har omtrent følgende parametere: øyets ekvator lengde (største omkrets av øyet i frontalplanet) - 23,6 mm, den optiske akse til lengde - 24 mm, den vertikale diameter av øyet - 23,4 mm. I en person som har slike standardparametre, vil krumningsradiusen være 8,6. Objektiver med priser fra 8,3 til 8,8 kan enkelt bli funnet på salg. Hvis krumningsradien i det vesentlige avviker fra normalverdiene, linsene må fremstilles på bestilling. Deres skisse er laget i samråd med en øyelege. Legen bestemmer en passende krumningsradius for den linsehjelpemiddel, som kalles "autorefractometry". Spesialisten undersøker hornhinnen i øynene ved hjelp av datadiagnostiske metoder. Prinsippet om infrarødt lysutslipp er grunnlaget for autorefraktometri. Det resulterende bildet av lysstrålen før det reflekteres fra netthinnen og etter at det er festet av spesielle sensorer. Også krumningsradien av linsens er definert som forskjellen i brytnings (brytende effekt i øyet optiske system, uttrykt i dioptrier) mellom øynene og mengden av astigmatisme (manglende evne til å fokusere perspektiv). Som fikseringspunktet bruker studien et uendelig fjernt bilde.Hva om kontaktlinsene ikke passer
I tilfelle linsene allerede er kjøpt, og radiuskrumning er ikke like, du må fortsette som følger. Hvis denne forskjellen ikke overstiger 0,2, anbefaler leger vanligvis å bruke slike linser, forutsatt at ubehag ikke følges. Hvis denne avviket overstiger 0,2, kan de ikke brukes. I tilfelle en person har mer konvekse kontaktlinser, vil deres mobilitet være vanskelig. Blodkar vil bli presset, dette vil uunngåelig føre til rødhet av øynene. Øyebollene vil være i konstant spenning, det kan være forstyrrelser i lakrimasjonen. Truselen mot betennelse vil øke, visjonen vil være ustabil. Hvis krumningsradiusen er høyere enn nødvendig indeks, vil kontaktlinsene være for mobile. De kan lett falle ut av øynene, skade hornhinnen, forårsake tåre. Flatlinser beveger seg lett bort fra hornhinnen, en person kan ikke se noe. Etter hvert som de har skadet øynets øvre muskler, vil det oppstå en blinkende smerte.Tips 12: Hvordan Eratosthenes beregnet jordens radius
Den legendariske gamle greske astronomen og matematikerenErastofen fastslår solens hellingsvinkel til jorden i to byer, som etter hans mening ligger på en meridian. Å kjenne avstanden mellom dem, beregnet han matematisk radien til planeten vår. Beregningene viste seg å være ganske nøyaktige.
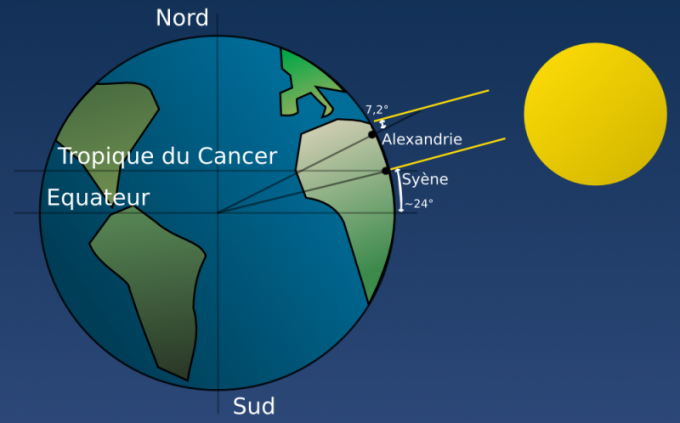
Metoden til Erastofen
Erastofen bodde i Alexandria,i nord i Egypt nær munnen av Nilen ved Middelhavskysten. Han visste at på en bestemt dag i hvert år i Siena i sør av Egypt på bunnen av brønnene var det ingen solskinn. Det er at Solen i det øyeblikket er rett over hodet. Men i Alexandria, som ligger nord for Siena, selv på sommerenes solstedsdag, er solen aldri direkte overhead. Erastofen innså at det er mulig å bestemme hvor langt solen er forskjøvet fra stillingen "rett over hodet" ved å måle vinkelen dannet av skyggen fra det vertikale objektet. Han målte lengden på skyggen fra det høye tårnet i Alexandria, og ved hjelp av geometri, beregnet vinkelen mellom skyggen og det vertikale tårnet. Det viste seg å være om lag 7,2 grader. Erastofen brukte mer komplekse geometriske konstruksjoner. Anta at vinkelen fra skyggen er nøyaktig den samme som mellom Alexandria og Siena, hvis du teller fra Jordens sentrum. For enkelhets skyld fant jeg ut at 7,2 grader er 1/50 av en full sirkel. For å finne jordens omkrets, ble avstanden mellom Siena og Alexandria multiplisert med 50. Ifølge Erastofen var avstanden mellom byene 5 tusen trinn. Men det var ingen generell lengdenhet i de tidlige tider, og i dag er det ikke kjent hvilket stadium Erastofen brukte. Hvis han brukte egypten, som var 157,5 m, var jordens radius 6287 km. Feilen i dette tilfellet var 1,6%. Og hvis du brukte det mer vanlige greske scenen, tilsvarer 185 m, ville feilen være 16,3%. I alle fall er nøyaktigheten av beregningene ganske bra for den tiden.Biografi og vitenskapelig aktivitet av Erastofen
Det antas at Erastofen ble født i 276 tilAD i byen Cyrene, som var på territoriet til moderne Libya. Han studerte i flere år i Athen. Han tilbrakte en betydelig del av sitt voksne liv i Alexandria. Han døde i 194 f.Kr. i en alder av 82 år. Ifølge noen versjoner sultet han selv til døden etter å være blind. I lang tid ledet Erastofen Alexandria-biblioteket, den mest berømte biblioteket i den antikke verden. I tillegg til det faktum at han beregnet størrelsen på planeten vår, gjorde han en rekke viktige oppfinnelser og funn. Fant en enkel metode for å bestemme primaltall, nå kalt "Erastofens sikt". Han tegnet et "verdens kart", der han viste alle deler av verden, kjent på den tiden til de gamle grekerne. Kortet ble ansett som en av de beste for sin tid. Utviklet et system med lengdegrad og breddegrad og en kalender som inkluderte sprangår. Fant armillary sfæren, en mekanisk enhet brukt av tidlige astronomer å demonstrere og forutsi den synlige bevegelsen av stjerner i himmelen. Også laget en stjernekatalog, som inkluderte 675 stjerner.Den greske forskeren Eratosthenes Kirensky for første gang i verden beregnet jordens radius Eratosthenes Beregning av jordens omkrets Eratosthenes







